Cristallographie

La cristallographie est la science qui se consacre à l'étude des cristaux à l'échelle atomique. Les propriétés physico-chimiques d'un cristal sont étroitement liées à l'arrangement spatial des atomes dans la matière. L'état cristallin est défini par un caractère périodique et ordonné à l'échelle atomique ou moléculaire. Le cristal est obtenu par translation dans toutes les directions d'une unité de base appelée maille élémentaire.

Elle est en rapport avec des disciplines aussi diverses que la physique, la chimie, l'optique, les mathématiques, la biophysique, la biologie, la médecine, la science des matériaux, la métallurgie ainsi que les sciences de la Terre.

Histoire

Le cristal, d'abord simple objet de curiosité, passionna les collectionneurs avant d'intriguer les savants qui, en étudiant sa structure, ébauchèrent les premières théories sur la constitution intime de la matière.

La loi des indices rationnels ou des troncatures simples fut définie par l'abbé René Just Haüy en 1774. Par observation du phénomène de clivage de la calcite, il a déterminé les « molécules intégrantes », c'est-à-dire les parallélépipèdes identiques constituant les cristaux et il en a déduit que chaque face d'un cristal peut être repérée dans l'espace par des nombres entiers.

Max von Laue obtient le prix Nobel de physique de 1914 « pour sa découverte de la diffraction des rayons X par des cristaux ». Commémorant ce centenaire, 2014 est proclamée « année internationale de la cristallographie » par l’Organisation des Nations unies^[1].

Les bases

La matière solide est composée d'atomes, que l'on peut voir comme des boules élémentaires, qui s'assemblent de plusieurs manières : reliées par des liaisons chimiques covalentes, les atomes forment une molécule, comme c'est le cas de gaz (ex. : le dioxygène O₂), de liquides (l'eau H₂O), de matériaux solides ou souples (ex. : polymères, caoutchoucs, plastiques, papiers, protéines… pouvant comporter des milliards de molécules semblables ou non en mélanges).

Les atomes (ou les molécules) peuvent s'agencer de manière irrégulière, on a alors de la matière dite « amorphe » (ou « vitreuse »), comme le verre (SiO₂). Enfin elles peuvent s'entasser de manière ordonnée, c'est alors un cristal (ex. : le quartz SiO₂). Dans ces cristaux non moléculaires, la structure est composée d'atomes ou d'ions qui forment un réseau tridimensionnel de polyèdres de coordination sans qu'aucune unité moléculaire n'existe : c'est le cas de la quasi-totalité des minéraux et de la majorité des cristaux inorganiques. Les cristaux de molécules (ex. : d'insuline) comportent des structures plus complexes.

Le cristal parfait et la maille élémentaire

Le « cristal parfait » est un modèle utilisé pour représenter la structure de la matière cristalline. Ce modèle considère qu'un cristal est un empilement ordonné et infini d'atomes, d'ions ou de molécules.

Le cristal est un solide à structure constituée d'atomes ordonnés dans un réseau périodique et même tripériodique et symétrique. Il a des propriétés de symétrie avec des axes de rotation directs et inverses, des miroirs, des plans et des centres de symétrie.

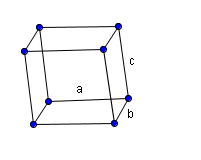
La maille cristalline élémentaire est le plus petit volume cristallin construit sur trois translations les plus courtes indépendantes du cristal. Elle est définie par trois vecteurs qui engendrent ainsi six paramètres de maille : les trois longueurs des vecteurs ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ et les trois angles entre ces vecteurs α, β, γ.

Symétrie

Le réseau cristallin

Un réseau est un ensemble de points ou « nœuds » en trois dimensions qui présente la propriété suivante : lorsque l'on se translate dans l‘espace selon certains vecteurs, on retrouve exactement le même environnement. Il y a donc une périodicité spatiale.

Il existe sept systèmes réticulaires de base : cubique, hexagonal, rhomboédrique, quadratique (ou tétragonal), orthorhombique, monoclinique et triclinique.

Le réseau de Bravais

Auguste Bravais définit, en 1848, à partir des différentes combinaisons des éléments de symétrie cristalline, 32 classes de symétrie, qui elles-mêmes se répartissent en 14 types de réseaux (il n'existe pas d'autre façon de disposer des points dans l'espace, afin de réaliser un réseau ou une maille, de manière à ne laisser aucun volume libre entre les réseaux). Les 14 réseaux de Bravais sont des expansions des 7 formes primitives de cristaux.

Voici deux exemples de réseaux de Bravais :

• Triclinique :

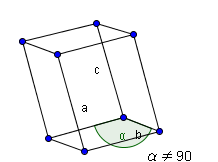
on a ${\displaystyle a}$ ≠ ${\displaystyle b}$ ≠ ${\displaystyle c}$ et aucun des angles n'est égal à 90°.

• Monoclinique :

Le deuxième réseau de Bravais est le réseau monoclinique. Celui-ci est composé de deux bases rectangulaires et de 4 faces ayant la forme de parallélogrammes. Les trois longueurs ${\displaystyle a}$, ${\displaystyle b}$ et ${\displaystyle c}$ ne sont pas égales : ${\displaystyle a}$ ≠ ${\displaystyle b}$ ≠ ${\displaystyle c}$, mais deux des trois angles sont égaux à 90º. On peut le trouver en réseau primitif (P ) ou en réseau à base rectangulaire centrée (C) (un nœud au milieu de la face définie par les axes a et b).

Groupes ponctuels de symétrie et groupes d'espace

Le groupe ponctuel de symétrie d'un système cristallin est le groupe (au sens mathématique) regroupant l'ensemble des opérations de symétrie qui laissent un nœud du réseau invariant. Ce nœud est donc situé à l'intersection de toutes les opérations de symétrie, dont la translation ne fait pas partie. Il existe 32 groupes ponctuels de symétrie distincts.

Le groupe d'espace d'un système cristallin regroupe l'ensemble des opérations de symétrie du groupe ponctuel, auxquelles s'ajoutent les opérations de translation. Vers 1890, Fedorov et Schoenflies démontrèrent — indépendamment l'un de l'autre — l'existence de 230 groupes d'espace, qui représentent toutes les combinaisons possibles de réseaux et d'opérations de symétrie.

Pour plus d'information, voir les articles :

• système cristallin ;
• groupe ponctuel de symétrie ;
• groupe d'espace.

Propriétés physiques

Par nature, tous les cristaux sont anisotropes. Mais cette anisotropie dépend des propriétés considérées.

• Propriétés optiques
  • À la lumière visible : transparence, réfraction, réflexion, diffraction, etc. Une grande partie des cristaux minéraux sont transparents, ce qui permet d'étudier leur réfraction. Seuls les cristaux cubiques sont isotropes, tous les autres étant anisotropes (indices de réfraction différents selon la direction d'observation). Par contre, les cristaux métalliques sont opaques à la lumière, ce qui ne permet que l'étude de leur réflexion. Pour étudier leur diffraction, il faut utiliser les rayons X.
  • Aux rayons X : voir cristallographie.

• Propriétés mécaniques : élasticité, dureté, résilience, etc.

Tous les cristaux sont anisotropes. (partie à compléter)

Les indices de Miller

Haüy a défini des indices (P, Q, R) qui permettent de repérer dans l'espace les faces d'un cristal. Miller, pour simplifier, a dit qu'il ne fallait pas utiliser P, Q et R mais leurs inverses (1/P, 1/Q, 1/R) qui seront notés h, k, l. Ils doivent être entiers naturels et de valeurs simples; si la maille utilisée pour décrire la symétrie du cristal est primitive, alors ils sont premiers entre eux.

Les défauts cristallins

La cristallogenèse

La cristallogenèse est la formation d'un cristal, soit en milieu naturel, soit de façon expérimentale.

Diffraction

Principe

Max von Laue eut l'idée d'irradier les cristaux avec des rayons X, car il pensait que le réseau cristallin ferait dévier le rayonnement de la même façon que la lumière est déviée dans certains minéraux transparents. L'expérience que des collègues réalisèrent sur un cristal de sulfate de cuivre lui permit de faire la démonstration de la structure périodique des empilements d'atomes dans les cristaux et de la nature ondulatoire du rayonnement X.

La détermination de la structure atomique d'un cristal s'effectue le plus souvent par diffraction des rayons X ou des neutrons, dont les longueurs d'onde sont de l'ordre des distances qui séparent les plans atomiques de la structure cristalline. Lorsque le cristal à étudier est irradié par un fin faisceau de rayons X, chacun des atomes du cristal diffuse une onde de faible amplitude, qui se propage dans toutes les directions. Les ondes issues des atomes interfèrent et donnent lieu à la diffraction, faisant apparaître sur le détecteur qui les reçoit des taches qui correspondent au maximum des ondes en phase ; les autres, en opposition de phase, s'annulent.

Réseau réciproque

Au niveau d'un écran situé à une distance des centres diffuseurs secondaires, on observera des figures de diffraction qui permettent de visualiser les perturbations créées par les interférences citées précédemment. Le réseau réciproque est l'image que l'on obtient à partir de la figure de diffraction.

Appareillage utilisé en cristallographie

• Le microscope polariseur analyseur
• Le diffractomètre

Applications

On utilise les propriétés de diffraction des cristaux en physique, chimie, biochimie, biologie, médecine et en sciences de la terre.

Leur analyse donne des informations sur des substances cristallines inorganiques et organiques (distance entre atomes, agencement spatial des atomes, identification de phases cristallines, taille des cristallites).

Annexes

Articles connexes

• Atome#Le modèle des sphères dures
• Constante de Madelung (pour les cristaux ioniques)
• Cristal de glace
• Cristallochimie
• André Guinier
• Quasicristal

Liens externes

• (en) Dictionnaire en ligne de cristallographie
• Association Française de Cristallographie
• Site web avec d'autres animations de physique des solides et physique quantique de l'Universite Paris Sud
• (en) Site web pour l'apprentissage de la Cristallographie, CSIC, Madrid

Notes et références

• Portail de la chimie
• Portail de la physique
• Portail des minéraux et roches
• Portail des sciences des matériaux