Analyse spectrale

En physique, l'analyse spectrale recouvre plusieurs techniques de description de signaux (variables selon le temps ou, plus rarement, dans l'espace) dans le domaine des fréquences. Elle permet en particulier d'obtenir les caractéristiques de la réponse d'un système linéaire en utilisant une fonction de transfert. En mathématiques, l'analyse harmonique correspond à une partie de ces techniques.

Présentation

Un phénomène physique dépendant du temps est décrit par un ou plusieurs signaux. On ne peut qu'exceptionnellement les interpréter de façon simple. Le problème est de trouver une description de leur contenu, relativement générale et adaptée aux problèmes concrets. Ceux-ci se présentent souvent de la manière suivante : un système transforme un signal d'entrée en un signal de sortie, comment déterminer les caractéristiques de celui-ci en fonction de celles du signal d'entrée et de celles du système ?

Dans le cas général, on ne connaît malheureusement pas la relation entre les valeurs du signal de sortie et celles du signal d'entrée mais seulement la relation entre les variations du signal de sortie et les valeurs (ou éventuellement les variations) du signal d'entrée. En termes mathématiques, le système est régi par une équation différentielle. Si celle-ci est quelconque, le problème est insoluble.

Heureusement, il existe une classe importante de systèmes, les systèmes linéaires (ou supposés tels) régis par le principe de superposition. Dans ce cas, correspondant à une équation différentielle linéaire, on peut essayer de décomposer le signal d'entrée en une somme de signaux simples auxquels on saurait faire correspondre des signaux de sortie également simples dont la somme donnerait le résultat cherché.

Le problème se simplifie encore plus si les caractéristiques du système restent constantes au cours du temps. On a affaire à une équation différentielle linéaire à coefficients constants. Les signaux simples sont les sinusoïdes qui subissent uniquement une amplification et un déphasage. C'est le problème de l'analyse spectrale : décomposer un signal compliqué en une somme de sinusoïdes.

Ici apparaît une difficulté car cette décomposition exige que le signal soit défini sur un temps infini. Or il ne peut être connu qu'à travers un enregistrement de durée limitée : il faut donc construire un modèle du signal en faisant des hypothèses, souvent évidentes intuitivement, sur la partie non enregistrée du phénomène.

Différents modèles

On peut supposer, par exemple, que le signal reproduit indéfiniment le contenu de l'enregistrement : on construit alors un modèle périodique basé sur la série de Fourier. Le signal est décrit par un spectre discret (ensemble de fréquences en progression arithmétique).

On peut aussi supposer que le niveau du signal est négligeable en dehors de l'enregistrement : on utilise dans ce cas un modèle transitoire basé sur la transformation de Fourier qui conduit en général à un spectre continu.

Il existe un certain nombre de phénomènes naturels pour lesquels aucune de ces deux hypothèses n'est réaliste. Par exemple, un enregistrement de vagues, sans montrer de périodicité, ne montre pas non plus de décroissance nette au cours de sa durée relativement faible : on parle alors de signal à variance finie (certains préfèrent parler de puissance finie mais ce n'est pas toujours pertinent techniquement), ce qui conduit à la notion de densité spectrale. On peut alors utiliser une hypothèse un peu plus floue selon laquelle la moyenne quadratique calculée sur l'enregistrement fournit une estimation raisonnable de la moyenne quadratique du signal. Ce type d'analyse conduit encore à un spectre continu. Il se définit, comme les précédents, à partir du signal mais on peut obtenir des informations supplémentaires en considérant celui-ci comme une réalisation d'un processus aléatoire.

Signaux périodiques

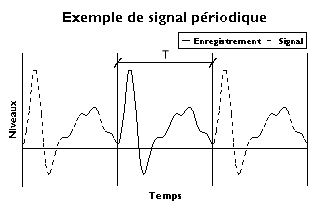
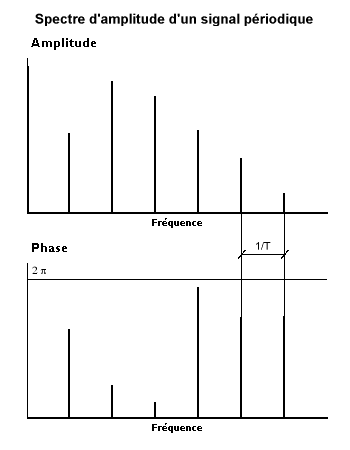
Le développement en série de Fourier d'un enregistrement de durée $T$ associe à celui-ci des sinusoïdes d'amplitudes finies et de fréquences multiples de la fréquence du fondamental ${\frac {1}{T}}$ . On parle d'un spectre d'amplitude qui est un spectre de raies. Dans le cas général, le résultat de l'analyse peut s'exprimer soit en amplitudes et phases, soit en composantes cosinus et sinus.

La sommation des sinusoïdes crée un signal périodique. Si le signal d'origine est périodique, il est parfaitement représenté – au moins en principe. Dans le cas contraire on n'a représenté que l'enregistrement et il faut tenter de trouver autre chose.

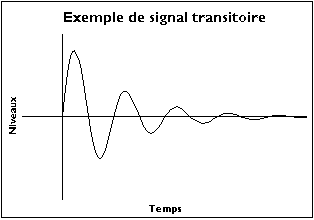
Signaux transitoires

Spectre densite amplitude signal transitoire.png

Ici, on raisonnera d'abord sur le signal de durée supposée infinie avant de voir les conséquences pour un enregistrement de durée finie. Si ce signal n'est pas périodique, n'a pas de période finie, on peut essayer de voir ce qui se passerait si on lui prêtait une période infinie. Cela entraîne les conséquences suivantes :

Lorsque la durée d'analyse $T$ tend vers l'infini, le pas de fréquence ${\frac {1}{T}}$ tend vers 0 : à la limite on passe d'un spectre discret à un spectre continu.
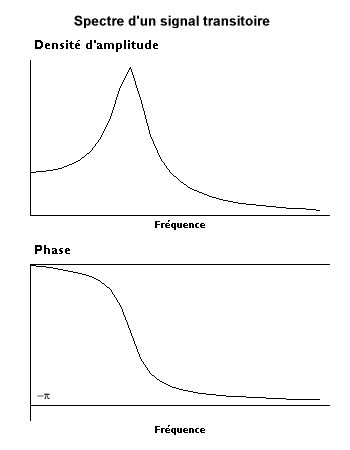
Au cours de cette croissance de la durée d'analyse, lorsque celle-ci est multipliée par un nombre n quelconque, le nombre de composantes est multiplié par le même facteur. Pour que le niveau du signal ne soit pas augmenté dans les mêmes proportions il faut que les amplitudes des composantes soient, en gros, divisées par n, ce qui risque de conduire à la limite à des amplitudes nulles. On pare cette difficulté en multipliant les coefficients de Fourier par la longueur d'analyse ou en les divisant par le pas de fréquence qui tend vers zéro. Ainsi, le spectre continu n'est plus un spectre d'amplitude mais un spectre de densité d'amplitude dont l'unité est unité physique / hertz.
Malgré ces précautions, la méthode peut diverger. Une condition de convergence est que le signal doit être transitoire : il doit tendre vers 0 lorsque le temps tend vers ± $\infty$ .

On obtient ainsi la transformée du signal $x(t)$ que l'on note généralement $X(f)$ , f étant la fréquence.

Si on retourne à un enregistrement de durée limitée, il y a deux possibilités :

Le signal n'est différent de zéro que pendant une durée limitée : l'analyse pendant cette durée fournit, au moins en principe, un résultat exact permettant de reconstituer le signal par inversion de la transformation ;
Le signal a des valeurs différentes de zéro pendant une durée supérieure à celle de l'enregistrement : l'imprécision du résultat croît avec la quantité d'information perdue. L'erreur ainsi commise se traduit concrètement par une dispersion de l'énergie correspondant à une fréquence sur les fréquences voisines et mathématiquement par la notion de convolution.

Signaux à variance finie

Le problème est plus compliqué que dans le cas précédent et on peut l'aborder de diverses manières. Celle que nous utiliserons n'est certainement pas la plus efficace d'un point de vue scientifique mais elle a l'avantage de montrer quelques points essentiels sans les cacher derrière des considérations mathématiques, sinon particulièrement difficiles, du moins assez lourdes. Pour s'affranchir de problèmes spécifiques liés à la prise en compte d'une moyenne non nulle, on supposera que le signal a été préalablement centré par soustraction de sa moyenne.

Fonction d'autocovariance

Étant donné un signal $x(t)$ , on appelle fonction d'autocovariance — souvent assimilée à tort à l'autocorrélation — la fonction de $\tau$ qui donne la moyenne des produits des valeurs de $x(t)$ à deux instants qui diffèrent de $\tau$ :

R_{x}(\tau )={\overline {x(t)x(t+\tau )}}

Dans le calcul de cette moyenne, t varie de $-\infty$ à $+\infty$ . Si le signal est transitoire, la fonction est nulle ; s'il est périodique, elle est elle-même périodique. En se plaçant dans le cas d'un signal qui n'appartient de toute évidence à aucune des deux catégories, la fonction possède les propriétés suivantes :

le changement de $\tau$ en $-\tau$ n'apporte aucune modification : la fonction est paire ;
à l'origine, $R_{x}(0)$ représente la variance qui est nécessairement positive ;
la symétrie impose qu'il s'agisse d'un extremum. En fait, il s'agit d'un maximum : si dans le calcul on remplace le décalage 0 par un petit décalage $\tau$ , à chaque franchissement du niveau 0, on remplace un petit produit positif par un petit produit négatif ;
en exceptant le cas du signal périodique, deux points séparés par un grand décalage $\tau$ ont peu de choses en commun : la fonction tend vers 0 lorsque ce décalage tend vers l'infini ;
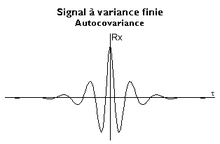
eu total, la fonction a souvent une vague allure de sinusoïde amortie ;
on veut, si c'est possible, assimiler le signal à une somme de sinusoïdes. Supposons que ce soit le cas. Que les amplitudes soient finies ou infiniment petites, on peut écrire cette somme sous la forme :

x(t)=\sum _{n}a_{n}\cos(\omega _{n}t+\varphi _{n})

Dans ces conditions on montre que

R_{x}(\tau )=\sum _{n}{a_{n}^{2} \over 2}\cos {\omega _{n}\tau }

Ainsi :

la fonction d'autocovariance contient les mêmes fréquences que le signal ;
les amplitudes ne sont pas identiques mais elles sont obtenues par élévation au carré et division par 2 ;
les phases ont entièrement disparu : l'autocovariance correspond non seulement au signal d'origine, mais aussi à tous ceux qui contiennent les mêmes composantes.

Densité spectrale

On peut déduire de ce qui précède :

la fonction d'autocovariance possède une transformée de Fourier que l'on nomme densité spectrale et que l'on note généralement $S_{x}(f)$ , f étant la fréquence ;
les composantes de l'autocovariance étant homogènes à des carrés d'amplitude, la densité spectrale est non négative. Elle a une dimension (unité physique)² / Hertz ;
l'autocovariance étant une fonction réelle et paire, sa transformée de Fourier possède les mêmes caractéristiques ;
un enregistrement tronquant toujours le signal censé se maintenir pendant un temps infini, la densité spectrale est nécessairement déformée par convolution.

Relation avec les processus aléatoires

À la déformation du contenu en fréquences déjà constatée pour les signaux transitoires s'ajoute une incertitude statistique liée à la position de l'enregistrement sur le signal.

La fonction d'autocovariance correspond à toute une famille de signaux qui contiennent les mêmes composantes. On peut interpréter cette famille comme celle des réalisations d'un processus continu. Un enregistrement de durée limitée peut également être considéré comme une réalisation d'un autre processus. Cela permet de préciser avec des intervalles de confiance la valeur statistique de l'analyse effectuée.

Voir aussi

Bibliographie

(en) Y. K. Lin, Probabilistic Theory of Structural Dynamics, New York, Robert E. Krieger Publishing Company, juillet 1976, 368 p. (ISBN 0-88275-377-0)

Navigation